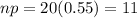Question

According to Harper's Index, 55% of all federal inmates are serving time for drug dealing. A random sample of 20 federal inmates is selected. (a) What is the probability that 11 or more are serving time for drug dealing? (Round your answer to three decimal places.) (b) What is the probability that 2 or fewer are serving time for drug dealing? (Round your answer to three decimal places.) (c) What is the expected number of inmates serving time for drug dealing? (Round your answer to one decimal place.)

Answer 1

a) P = 0.591

b) P = 0.0000358

c) 11 inmates

Explanation:

This is a binomial distribution exercise.

Where p = 0.55 is the success probability

The random variable is X : ''number of inmates serving time for drug dealing''

X ~ Bi(n;p)

Where n is the random sample and p is the success probability

The probability function is :

`P(X=x)=f(x)=nCx.p^(x).(1-p)^(n-x)`

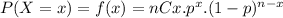
Where nCx is the combinatorial number define as

`nCx=(n!)/(x!(n-x)!)`

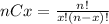
a)
`P(X\geq 11) =f(11)+f(12)+f(13)+f(14)+f(15)+f(16)+f(17)+f(18)+f(19)+f(20)`

`P(X\geq 11)=0.1771+0.1623+0.1221+0.0746+0.0365+0.0139+0.004+0.0008+0.0001+0.55^(20)`

`P(X\geq 11)=0.591`

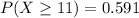
b)

`P(X\leq 2)=f(0)+f(1)+f(2)=0.0000358`

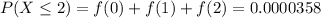
c) The expected number for X is

`np=20(0.55)=11`