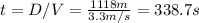Answer:
a) 10.29° upstream
b) t=338.7s
Step-by-step explanation:
If the river is 1km wide and the destination point is 0.5km away downstream, then the angle and distance the the boat has to travel is:
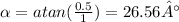
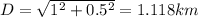
The realitve velocity of the boat respect to the water is:
![V_(B/W)=[3*cos\beta ,3*sin\beta ]](https://img.qammunity.org/2020/formulas/physics/college/5yt1eii1cvgk0x7bsewefq93borrt09ojx.png) where β is the angle it has to be pointed at.
where β is the angle it has to be pointed at.
From the relative mvement equations:
 where
where
![V_B=[V*cos\alpha ,-V*sin\alpha ]](https://img.qammunity.org/2020/formulas/physics/college/ah007f8bdoxzit5lxhpwxgwlr5eyij3fnf.png)
From this equation we get one equation per the x-axis and another for the y-axis. If we square each of them and add them together, we will get 2 equations:
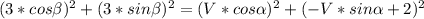
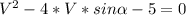 Solving for V:
Solving for V:
V = 3.3m/s and V=-1.514m/s Replacing this value into one of our previous x or y-axis equations:
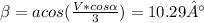
The amount of time: