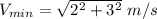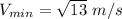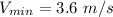Question

The origin is on flat ground, and the z-axis points upward. For time 0 ≤ t ≤ 10, a particle moves along a path given by ⃗r(t) = 2ti + 3tj + (100 − (t − 5)2 ) ⃗k. For what time(s) 0 ≤ t ≤ 10 is the particle at its highest point and what is its position then? For what time(s) 0 ≤ t ≤ 10 is the particle moving fastest? What is the fastest speed? For what time(s) 0 ≤ t ≤ 10 is the particle moving slowest? What is the slowest speed?

Answer 1

t= 5 s the particle will be on the highest position.

`r(t) = 10i + 15j + 100k`

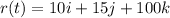
The maximum values of particle will at t= 10 s

`V_(max)=10.63\ m/s`

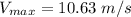
The minimum values of particle will at t= 5 s

`V_(min)=3.6 \ m/s`

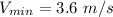
Step-by-step explanation:

Given that

`r(t) = 2ti + 3tj + (100-(t- 5)^2)k`

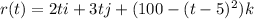
Time when the particle will be on the highest position:

When the Z component of r(t) will be maximum then the particle will be on the highest position.

`Z=(100-(t- 5)^2)`

`(dZ)/(dt)=0-2(t-5)`

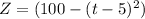
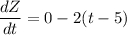
It means at t= 5 s the particle will be on the highest position.

Position at t= 5

`r(t) = 2ti + 3tj + (100-(t- 5)^2)k`

`r(t) = 2* 5i + 3* 5j + (100-(5- 5)^2)k`

`r(t) = 10i + 15j + 100k`

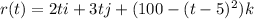
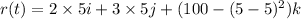
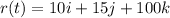
Speed :

`V=(dr)/(dt)`

`V=2i + 3j -2(t- 5)k`

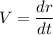
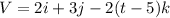
The maximum values of particle will at t= 10 s

`V_(max)=√(2^2+3^2+10^2) \ m/s`

`V_(max)=√(113) \ m/s`

`V_(max)=10.63\ m/s`

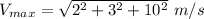
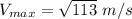
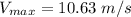
The minimum values of particle will at t= 5 s

`V_(min)=√(2^2+3^2) \ m/s`

`V_(min)=√(13) \ m/s`

`V_(min)=3.6 \ m/s`