Question

The "Giant Swing" at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable 5.00 m long, the upper end of the cable being fastened to the arm at a point 3.00 m from the central shaft. Does the angle depend on the weight of the passenger for a given rate of revolution?

Answer 1

In the expression the mass is cancelled out and angle is independent of the weight of the person

Step-by-step explanation:

Let the swing is rotating with constant angular speed

now due to rotation of swing the string will make some angle with the vertical

now we have

`Tcos\theta = mg`

`T sin\theta = m\omega^2 r`

now we will have

`tan\theta = (\omega^2 r)/(g)`

here we know that

`r = R + L sin\theta`

where

R = 3.00 m

L = 5.00 m

Now as we can see the above expression the mass is cancelled out and angle is independent of the weight of the person

Answer 2

Step-by-step explanation:

When the central shaft rotates , the seat along with passenger also rotates . Their rotation requires a centripetal force of mw²R where m is mass of the passenger and w is the angular velocity and R is radius of the circle in which the passenger rotates.

This force is provided by a component of T , the tension in the rope from which the passenger hangs . If θ be the angle the rope makes with horizontal ,

T cos θ will provide the centripetal force . So

Tcosθ = mw²R

Tsinθ component will balance the weight .

Tsinθ = mg

Dividing the two equation

Tanθ =
`(g)/(\omega^2R)`

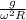
Hence for a given w , θ depends upon g or weight .