Question

When you purchased your​ car, you took out a​ five-year annual-payment loan with an interest rate of 5.8 % per year. The annual payment on the car is $ 4 comma 700. You have just made a payment and have now decided to pay off the loan by repaying the outstanding balance. What is the payoff amount for the following​ scenarios? a. You have owned the car for one year​ (so there are four years left on the​ loan)? b. You have owned the car for four years​ (so there is one year left on the​ loan)?

Answer 1

To calculate the payoff amount for a car loan with one year left, use an amortization formula with the remaining years and interest rate. Substitute the values into the formula to find the remaining balance, which is the payoff amount.

Step-by-step explanation:

To calculate the payoff amount for a car loan, we need to consider the remaining years on the loan and the interest rate. In this scenario, the loan term is 5 years, and you have owned the car for 4 years, so there is 1 year left on the loan. We'll use an amortization formula to calculate the remaining balance:

Remaining balance = Loan amount × (1 + Interest rate)^Remaining years - (Payment per year × ((1 + Interest rate)^(Remaining years) - 1) ÷ Interest rate)

For this case, the calculation would be:

Remaining balance = $4,700 × (1 + 0.058)^1 - ($4,700 × ((1 + 0.058)^1 - 1) ÷ 0.058)

After evaluating the formula, the payoff amount would be the remaining balance.

Answer 2

after the first quota carrying value: 16.360,85‬

after the fourht quota carrying value: 4,442.34

Step-by-step explanation:

we calculate the present valeu of the payment to know the value of the car:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 4,700

time 5

rate 0.058

`4700 * (1-(1+0.058)^(-5) )/(0.058) = PV\\`

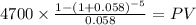
PV $19,906.29

Nowe to know the princpal after first payment we need to know the first quoa maortization:

19,906.29 x 0.058 = 1,154.56 interest

quota - interest

4,700 - 1,154.56 = 3,545.44‬

19,906.29 - 3,545.44 = 16.360,85‬

now the last cuota, the discounted value of the cuopa will be the amount of principal we owe as afterthis payment the loan is cancelled.

`(Maturity)/((1 + rate)^(time) ) = PV`

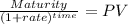
Maturity 4,700.00

time 1.00

rate 0.058

`(4700)/((1 + 0.058)^(1) ) = PV`

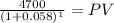
PV 4,442.34