Question

At one point the average price of regular unleaded gasoline was ​$3.43 per gallon. Assume that the standard deviation price per gallon is ​$0.07 per gallon and use​ Chebyshev's inequality to answer the following. ​(a) What percentage of gasoline stations had prices within 4 standard deviations of the​ mean? ​(b) What percentage of gasoline stations had prices within 1.5 standard deviations of the​ mean? What are the gasoline prices that are within 1.5 standard deviations of the​ mean? ​(c) What is the minimum percentage of gasoline stations that had prices between ​$3.22 and ​$3.64​?

Answer 1

(a) The percentage of gasoline stations had prices within 4 standard deviations of the​ mean is 93.75%.

(b) The percentage of gasoline stations had prices within 1.5 standard deviations of the​ mean is 55.56%. The prices for this stations goes from $3.325 to $3.535.

(c) The minimum percentage of stations that had prices between ​$3.22 and ​$3.64 is 88.88%.

Explanation:

The Chebyshev's inequality states that at least 1-(1/K^2) of data from a sample must fall within K standard deviations from the mean, being K any positive real number greater than one.

It can be expressed as

`P(|X-\mu| \geq k\sigma)\leq (1)/(k^2)`

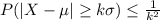
In this problem, we have, for the gasoline price, a normal distribution with mean of 3.43 and standar deviation of 0.07.

(a) The percentage of gasoline stations had prices within 4 standard deviations of the​ mean is equal to one less the percentage of gasoline stations that had prices out of 4 standard deviations of the​ mean:

`P(|X-\mu| \leq k\sigma)=1-P(|X-\mu| \leq k\sigma) \\\\1-P(|X-\mu| \leq k\sigma) \geq 1-(1)/(k^2) \\\\1-P(|X-\mu| \leq 4\sigma) \geq 1-(1)/(4^2)\\\\1-P(|X-\mu| \leq 4\sigma) \geq 1-1/16\\\\1-P(|X-\mu| \leq 4\sigma) \geq 0.9375`

The percentage of gasoline stations had prices within 4 standard deviations of the​ mean is 93.75%.

(b) The percentage of gasoline stations had prices within 1.5 standard deviations of the​ mean is 55.56%.

`P(|X-\mu| \leq k\sigma)\geq 1-(1)/(k^2)\\\\P(|X-\mu| \leq 1.5\sigma)\geq 1-(1)/(1.5^2)\\\\P(|X-\mu| \leq 1.5\sigma)\geq 0.5556\\`

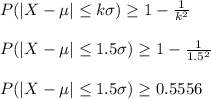
The prices for this stations goes from $3.325 to $3.535.

`X=\mu\pm 1.5\sigma=3.43\pm 1.5*0.07=3.43 \pm 0.105\\\\X_(upper) =3.43+0.105=3.535\\X_(lower)=3.43-0.105=3.325`

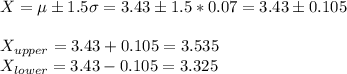
(c) To answer, we have to calculate k for this range of prices:

`x=\mu\pm k\sigma\\\\k=(|x-\mu|)/(\sigma) =(|3.64-3.43|)/(0.07)=(0.21)/(0.07)=  3`

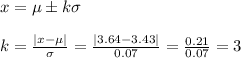
For k=3, the Chebyshev's inequality states:

`P(|X-\mu| \leq 3\sigma)\geq 1-(1)/(3^2)\\\\P(|X-\mu| \leq 3\sigma)\geq 0.8889`

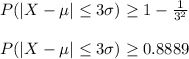
So, the minimum percentage of stations that had prices between ​$3.22 and ​$3.64 is 88.88%.