Question

Be sure to answer all parts. Write the balanced equations corresponding to the following rate expressions: a) rate = − 1 3 Δ[CH4] Δt = − 1 2 Δ[H2O] Δt = − Δ[CO2] Δt = 1 4 Δ[CH3OH] Δt (Click in the answer box to activate the palette. Do not include states of matter.) b) rate = − 1 2 Δ[N2O5] Δt = 1 2 Δ[N2] Δt = 1 5 Δ[O2] Δt (Click in the answer box to activate the palette. Do not include states of matter.) c) rate = − 1 2 Δ[H2] Δt = − 1 2 Δ[CO2] Δt = − Δ[O2] Δt = 1 2 Δ[H2CO3] Δt (Click in the answer box to activate the palette. Do not include states of matter.)

Answer 1

Answer : The balanced equations will be:

(a)
`3CH_4+2H_2O+CO_2\rightarrow 4CH_3OH`

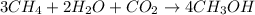
(b)
`2N_2O_5\rightarrow 2N_2+5O_2`

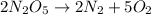
(c)
`2H_2+2CO_2+O_2\rightarrow 2H_2CO_3`

Explanation :

The general rate of reaction is,

`aA+bB\rightarrow cC+dD`

Rate of reaction : It is defined as the change in the concentration of any one of the reactants or products per unit time.

The expression for rate of reaction will be :

`\text{Rate of disappearance of A}=-(1)/(a)(d[A])/(dt)`

`\text{Rate of disappearance of B}=-(1)/(b)(d[B])/(dt)`

`\text{Rate of formation of C}=+(1)/(c)(d[C])/(dt)`

`\text{Rate of formation of D}=+(1)/(d)(d[D])/(dt)`

`Rate=-(1)/(a)(d[A])/(dt)=-(1)/(b)(d[B])/(dt)=+(1)/(c)(d[C])/(dt)=+(1)/(d)(d[D])/(dt)`

From this we conclude that,

In the rate of reaction, A and B are the reactants and C and D are the products.

a, b, c and d are the stoichiometric coefficient of A, B, C and D respectively.

The negative sign along with the reactant terms is used simply to show that the concentration of the reactant is decreasing and positive sign along with the product terms is used simply to show that the concentration of the product is increasing.

Now we have to determine the balanced equations corresponding to the following rate expressions.

(a)
`Rate=-(1)/(3)(d[CH_4])/(dt)=-(1)/(2)(d[H_2O])/(dt)=-(d[CO_2])/(dt)=+(1)/(4)(d[CH_3OH])/(dt)`

The balanced equations will be:

`3CH_4+2H_2O+CO_2\rightarrow 4CH_3OH`

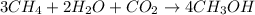
(b)
`Rate=-(1)/(2)(d[N_2O_5])/(dt)=+(1)/(2)(d[N_2])/(dt)=+(1)/(5)(d[O_2])/(dt)`

The balanced equations will be:

`2N_2O_5\rightarrow 2N_2+5O_2`

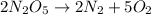
(c)
`Rate=-(1)/(2)(d[H_2])/(dt)=-(1)/(2)(d[CO_2])/(dt)=-(d[O_2])/(dt)=+(1)/(2)(d[H_2CO_3])/(dt)`

The balanced equations will be:

`2H_2+2CO_2+O_2\rightarrow 2H_2CO_3`