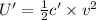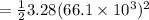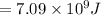Question

Each of the laser gun most favored by Rosa the Closer, the intrepid vigilante of the lawless 22nd century, is powered by the discharge of a 1.69 F capacitor charged to 66.1 kV . Rosa rightly reckons that she can enhance the effect of each laser pulse by increasing the electric potential energy of the charged capacitor. She could do this by replacing the capacitor's filling, whose dielectric constant is 489 , with one possessing a dielectric constant of 951 . Find the electric potential energy of the original capacitor when it is charged. original capacitor potential energy:

Answer 1

Potential Energy of capacitor is
`= 7.09* 10^9 J`

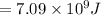
Step-by-step explanation:

Given data:

Capacitance C = 1.69 F

Voltage
`V = 66.1 kV = 66.1 * 10^3 V`

Initial dielectric constant
`k_1 = 489`

New dielectric constant
`K_2 = 951`

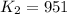
a) potential energy of capacitor

`U = (1)/(2) cv^2`

`= (1)/(2) 1.69 (66.1* 10^3)^2`

`= 3.69* 10^9 J`

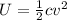
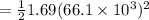
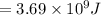
b) Upgraded capacitance
`C' = c(k_2)/(k_1)`

`= 1.69 * (951)/(489) = 3.28 F`

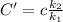
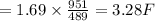
Potential Energy of capacitor is

`U' =(1)/(2) c' * v^2`

`= (1)/(2) 3.28 (66.1* 10^3)^2`

`= 7.09* 10^9 J`