Question

A woman can row a boat at 5.60 km/h in still water. (a) If she is crossing a river where the current is 2.80 km/h, in what direction must her boat be headed if she wants to reach a point directly opposite her starting point? Express your answer as an angle with respect to the line perpendicular to the river, positive if down the river. (b) If the river is 5.60 km wide, how long will she take to cross the river? (c) Suppose that instead of crossing the river she rows 2.80 km down the river and then back to her starting point. How long will she take? (d) How long will she take to row 2.80 km up the river and then back to her starting point? (e) In what direction should she head the boat if she wants to cross in the shortest possible time, and (f) what is that time?

Answer 1

a) θ = 30°

b) t = 1.154 h

c) ttotal = 1.33 h

d) ttotal = 1.33 h

e) cross the river in the shortest time possible, that angle must be equal to zero, where the cosine component is maximized.

f) t = 1 h

Step-by-step explanation:

a) the total speed is equal to:

v = vw + vc

the direction is equal to:

θ = sin^-1(vc/vw), replacing values:

θ = sin^-1(2.8/5.6) = 30°

b) The time taken is equal to:

t = (5.6/(v*cosθ)) = (5.6/(5.6*cos30°)) = 1.154 h

c) The total time is equal to:

ttotal = t1 + t2 = (L/(vw + vc)) + (L/(vw-vc))

ttotal = (2.8/(5.6+2.8)) + (2.8/(5.6-2.8)) = 1.33 h

d) The total time is equal to:

ttotal = t1 + t2 = (L/(vw + vc)) + (L/(vw-vc))

ttotal = (2.8/(5.6+2.8)) + (2.8/(5.6-2.8)) = 1.33 h

e) cross the river in the shortest time possible, that angle must be equal to zero, where the cosine component is maximized.

f) The shortest time is equal to:

t = (5.60/(5.60*cos0°)) = 1 h

Answer 2

a) θ=210°, b) t=1.155hr, c) t=1.333hr, d) t=1.333hr, e) θ=180° (straight across), f) t=1hr.

Step-by-step explanation:

So, the very first thing we nee to do when solving this problem is draw a diagram that represents it. In the attached picture I show a diagram for each part of this problem.

part a)

So, for her to move in a direction directly opposite her starting point, the x-component of her velocity must be de same as the velocity of the river in the opposite direction. We can use this fact to find the angle we need. If we analize the triangle I drew in the diagram, we can ses that:

`cos \theta = \frac {V_(river)}{V_(boat)}`

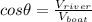
When solving for theta, we get that:

`\theta =cos^(-1) ( \frac {V_(river)}{V_(boat)})`

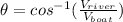
so now we can substitute the corresponding values:

`\theta =cos^(-1) ( \frac {2.80km/hr}{5.60km/hr}})`

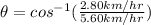
Which yields:

`\theta = 60^(o)`

but we are measuring the angle relative to the line perpendicular to the river, positive if down the river. So we need to subtract the angle from 270° so we get:

θ=270°-60°=210°

part b)

for part b, we need to find what the y-component for the velocity of the boat is for an angle of 210° as shown in the problem, so we get that:

`V_(y)=5.60km/hr*cos(210^(o))`

`V_(y)=-4.85km/hr`

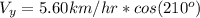
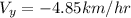
The woman will head in a negative 5.60km distance from one side to the other, so we get that the time it takes her to go to the other side of the river is:

`t=(y)/(V_(y))`

`t=(5.60km)/(4.85km/hr)=1.155hr`

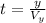
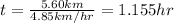
part c)

In order to find the time it takes her to travel 2.80km down and up the river, we need to find the velocities she will have in both directions. First, down stream:

`V_(ds)=V_(river)+V{boat}`

`V_(ds)=2.80km/hr+5.60km/hr=8.40km/hr`

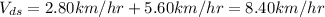
and now up stream:

`V_(us)=V_(boat)-V{river}`

`V_(us)=5.60km/hr-2.80km/hr=2.80km/hr`

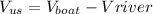
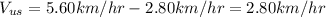
Once we got these two velocities we will now need to find the time to take each trip:

time down stream:

`t_(ds)=(x)/(v_(ds))`

`t_(ds)=(2.80km)/(8.40km/hr)=0.333hr`

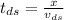
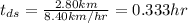
and the time up stream:

`t_(us)=(x)/(v_(us))`

`t_(us)=(2.80km)/(2,80km/hr)=1hr`

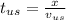
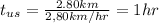
so the total time will be:

`t_(ds)+t_(us)=0.333hr+1hr=1.333hr`

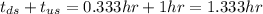
d) the time it takes the boat to go upstream and then downstream for the same distance is the same as the time we got on part c, since both times will be the same but they will come in different order, but their sum will be just the same:

t=1.333hr

e) For her to cross the river faster, she must row in a 180° direction (this is in a direction straight accross the river) that way she will use all her velocity to move across the river. (Even though she will move a certain distance horizontally and will not reach a point opposite to the starting point.)

f) In order to find the time it takes her to get to the other side, we need to divide the distance into the velocity of the boat.

`t=(d)/(v_(boat))`

`t=(5.60km)/(5.60km/hr)`

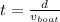
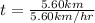
so

t= 1hr