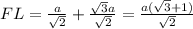Answer:
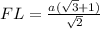
Explanation:
As given in figure 1 below:
FK = a, m∠F = 45° and m∠L = 30°
Construction: Draw an altitude KE from point K on FL.
Now, In ΔFEK,
FE = EK (Sides opposite to equal angles of a triangle)
Let FE = EK = x
Now, using pythagoras In ΔFEK,
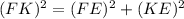
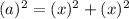
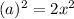
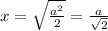
∴ FE = EK =
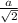
Now in ΔEKL, EK =
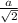
Using trigonometry ratio,
TanФ = Altitude\ Base
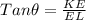
Tan 30° =
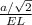
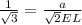
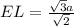
Now FL = FE + EL
FE =
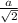 and
and
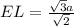
∴