Question

You are saving for retirement. To live​ comfortably, you decide you will need to save $ 2 million by the time you are 65. Today is your 23 rd ​birthday, and you​ decide, starting today and continuing on every birthday up to and including your 65 th ​birthday, that you will put the same amount into a savings account. If the interest rate is 5 %​, how much must you set aside each year to make sure that you will have $ 2 million in the account on your 65 th ​birthday?

Answer 1

Using the formula for the future value of an annuity, we can determine the annual payment needed to reach $2 million by age 65. With a 5% annual interest rate and 43 years to save, the calculation will reveal the required annual contribution. Starting early capitalizes on the exponential growth provided by compound interest.

Step-by-step explanation:

To determine how much one must save each year to have $2 million by the time they are 65, we can use the formula for the future value of an annuity. Since the interest is compounded annually, and the same amount is deposited on each birthday, we have an ordinary annuity. The future value FV of an ordinary annuity is calculated using the formula:

FV = P × (
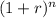`(1 + r)^n` - 1) / r

Where:

• FV = Future Value of the annuity, which is $2,000,000
• P = Annual payment (what we want to find out)
• r = Annual interest rate (5% or 0.05)
• n = Total number of payments (from 23 to 65 years old is 43 payments)

Substituting the values we get:

$2,000,000 = P × (
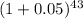`(1 + 0.05)^(43)` - 1) / 0.05

This formula can be rearranged to solve for P (the annual payment):

P = $2,000,000 / ((
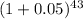`(1 + 0.05)^(43 )`- 1) / 0.05)

After calculating, we find the value of P required to achieve the $2 million goal.

The power of compound interest significantly impacts retirement savings, as shown through an example where an initial investment grows exponentially over time. Starting to save early in life with a consistent investment strategy allows for a lower annual contribution due to the effect of compound growth.

Answer 2

Annual deposit= $14,789.43

Step-by-step explanation:

Giving the following information:

You decide you will need to save $ 2 million by the time you are 65.

The interest rate is 5 %​. The number of years until 65 is 42.

We need to use the following Final Value formula:

FV= {A*[(1+i)^n-1]}/i

A= annual deposit

Isolating A:

A= (FV*i)/{[(1+i)^n]-1}

A= (2000000*0.05)/[(1.05^42)-1]= $14,789.43