Answer:
The total numbers of possible combinations are 3430.
Explanation:
Consider the provided information.
A combination for 0 1 2 3 4 6 5 7 8 9 this padlock is four digits long. Because of the internal mechanics of the lock, no pair of consecutive numbers in the combination can be the same or one place apart on the face.
Here, for the first digit we have 10 choices.
For the second digit we have 7 choices, as the digit can't be the same nor adjacent to the first digit.
For the third digit we have 7 choices, as the digit can't be the same nor adjacent to the second digit.
For the fourth digit we have 7 choices, as the digit can't be the same nor adjacent to the third digit.
So the number of choices are:
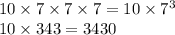
Hence, the total numbers of possible combinations are 3430.