Question

A company selling licenses of new e-commerce software advertised that firms using this software could obtain, on average during the first year, a minimum yield (in cost savings) of 20 percent on average on their software investment. To disprove the claim, we checked with 10 different firms which used the software. These firms reported the following cost-saving yields (in percent) during the first year of their operations: {17.0, 19.2, 21.5, 18.6, 22.1, 14.9, 18.4, 20.1, 19.4, 18.9}. a. Do we have significant evidence to show that the software company’s claim of a minimum of 20 percent in cost savings was not valid? Test using α = 0.05. b. Compute a 95% confidence interval for the average cost-saving yield estimate.

Answer 1

(a) We have not significant evidence to show that the software company's claim of a minimun of 20 percent in cost savings was not valid

(b) a 95% confidence interval for the average cost-saving yield is (17.5283, 20.4917)

Explanation:

Let X be the random variable that represents a cost-saving yield (in percent) during the first year of operation of the software for a firm. We have observed n = 10 values,
`\bar{x}` = 19.01 and s = 2.0712. We suppose that X is normally distributed.

(a)

We have the following null and alternative hypothesis

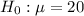`H_(0): \mu = 20` vs
`H_(1): \mu < 20` (lower-tail alternative)

We will use the test statistic

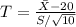`T = \frac{\bar{X}-20}{S/√(10)}` and the observed value is

`t = (19.01-20)/(2.0712/√(10)) = -1.5115`

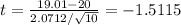
if
`H_(0)` is true, then T has a t distribution with n-1 = 9 degrees of freedom.

p-value = P(T < -1.5115) = 0.0825

We can use a table from a book or a programming language to find this probability P(T < -1.5115).

You can use the instruction pt(-1.5115, df = 9) in the R statistical programming language.

Because the p-value is greater than 0.05 (0.0825 > 0.05) we fail to reject the null hypothesis at the level of significance of 0.05.

(b)

We will use

`T = \frac{\bar{X}-\mu}{S/√(n)}`

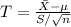
as the pivotal quantity. T has a
`t` distribution with n-1 = 9 degrees of freedom. Then, as we want a 95% confidence interval for the average cost-saving yield estimate, we should find the 2.5th quantile of the t distribution with 9 degrees of freedom, i.e.,
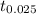`t_(0.025)`, this value is -2.2622. Therefore the 95% confidence interval is given by

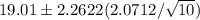`19.01\pm 2.2622(2.0712/√(10))`, i.e.,

(17.5283, 20.4917)

To find the 2.5th quantile of the t distribution with 9 degrees of freedom, you can use a table from a book or the next instruction in the R statistical programming language

qt(0.025, df = 9)