Question

A titration is performed to calculate the concentration of a solution of a monoprotic acid. The buret is filled with a standardized solution of 158.32 ± 0.05 mM NaOH. The initial volume is recorded as 0.14 mL. 25.00 mL of the unknown acid solution are pipetted into an Erlenmeyer flask and the solution is titrated to a phenolphthalein endpoint. The final buret reading is 18.76 mL. Assuming that the error in each volumetric measurement (buret and pipet) is ±0.03 mL, calculate the concentration of the acid (mM) and use propagation of error to estimate its uncertainty.

Answer 1

The concentration of the acid is 117.92 ± 0.03 mM.

Step-by-step explanation:

In this problem, the concentration of NaOH and the volume used is given. The volume pipetted from the acid is also given. The concentration of the acid is given by:

CNaOH * VNaOH = Cacid * Vacid

158.32 * (18.76-0.14) = C acid * 25

C acid = 117.92 mM

The propagation of error for this problem, which is a multiplication is the concentration of the acid multiplied by the error divided by its respective value as shown in the equation below

error = 117.92 *
`\sqrt{(0.05)/(158.32)^(2) +(0.03)/(18.62)^(2) +(0.03)/(25)^(2) }`

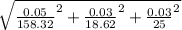
The answer is 0.03 mM of uncertainty.