Question

Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x->0.1^- 10x-1/|10x^3-x^2|

Answer 1

let's change some the 0.1 to say 1/10, just the fraction version of it.

`\bf \lim\limits_{x\to \left( (1)/(10) \right)^-}~\cfrac{10x-1}\implies \lim\limits_{x\to \left( (1)/(10) \right)^-}~\cfrac{10(-x)-1}{10(-x)^3-(-x)^2}`

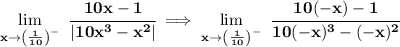
`\bf \cfrac{-10x-1}{-10x^3-x^2}\implies \cfrac{-10\left( (1)/(10) \right)-1}{-10\left( (1)/(10) \right)^3-\left( (1)/(10) \right)^2}\implies \cfrac{-1-1}{-(1)/(100)-(1)/(100)}\implies \cfrac{-2}{(-2)/(100)} \\\\\\ \cfrac{~~\begin{matrix} -2 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}{1}\cdot \cfrac{100}{~~\begin{matrix} -2 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}\implies 100`

when checking an absolute value expression, we do the one-sided limits, since an absolute value expression is in effect a piecewise function with ± versions, so for the limit from the left we check the negative version.