Answer with Explanation:
We are given that
Diameter=0.030 m
Length of sprue=
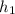 =0.200 m
=0.200 m
Metal volume flow rate,Q=0.03
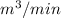
Q=
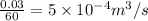 because 1 minute=60 seconds
because 1 minute=60 seconds
Let 1 for the top and 2 for the bottom
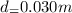
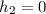
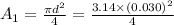
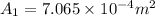
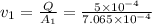
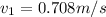
Pressure at the top and bottom of the sprue is atmospheric
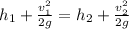
Substitute the values
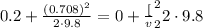
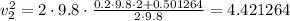
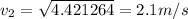
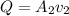
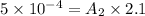
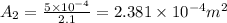
Reynolds number=
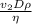
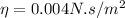
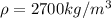
Substitute the values then we get
Reynolds number=
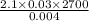
Reynolds number=42525
The Reynolds number is greater than 4000 .Therefore, the flow is turbulent.