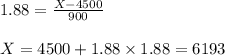Question

A warehouse distributor of carpet faces a normally distributed demand for its carpet. The average demand for carpet from the stores that purchase from the distributor is 4,500 yards per month, with a standard deviation of 900 yards. a. Suppose the distributor keeps 6,000 yards of carpet in stock during a month. What is the probability that a customer’s order will not be met during a month? (This situation is referred to as a stockout.) b. What is the probability that the demand will be between 5000 and 7000 yards? c. How many yards of carpet should this warehouse distributor order from its supplier to ensure that 97% of the demand is met? (The percent of customer demand/orders satisfied is referred to as service level. In this question, the service level is 97%.)

Answer 1

Answer with Step-by-step explanation:

Since the demand is normally distributed the required probability can be found from the area under the normal distribution curve as

Part a)

Given mean = 4500 yards per month

Standard deviation = 900 yards

Thus area under the curve corresponding to 6000 yards is found from the standard variate factor Z as

`Z=\frac{X-\bar{X}}{\sigma }\\\\Z=(6000-4500)/(900)=1.67`

Area for Z = 1.67 = 95.22%

Thus the probability that the demand will be met is 0.9522 hence the probability that the demand will not be met is
`P(E)=1-0.9522=0.0478`

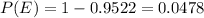
Part b)

The reuired answer is area between 5000 and 7000 yards in the normal distribution curve thus we have

`Z_1=(5000-4500)/(900)=0.56`.

`Z_2=(7000-4500)/(900)=2.78`

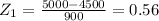The area between these 2 values is 49.73% hence the reuired probability is 0.4973.

Part c)

For 97% satisfaction of demand the Z factor corresponding to 97% of area is found to be 1.88

thus we can write

`1.88=(X-4500)/(900)\\\\X=4500+1.88* 1.88=6193`