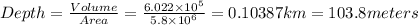Question

One thousand tonnes (1000 t, one t equals 10 cubed kg) of sand contains about a trillion (10 super 12) grains of sand. How many tonnes of sand are needed to provide 1 mol of grains of sand? (b) Assuming the volume of a grain of sand is 1.0 mm3 and the land area of the continental United States is 3.6 multiplication 10 super six square miles, how deep would the sand pile over the United States be if this area were evenly covered with 1.0 mol of grains of sand?

Answer 1

Answer with Step-by-step explanation:

Since 1 mole of sand will contain Avagadro's Number of sand particles (by definition of 1 mole)

Thus we have

1 mole of sand =
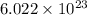`6.022* 10^(23)` sand particles

Thus in number of trillion sand particles we have no of trillion sand particles in 12 mole is

`(6.022* 10^(23))/(10^(12))=6.022* 10^(11)`

Now since it is given that mass of 1 trillion sand particles is 1000 tonnes Thus the mass of
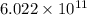`6.022* 10^(11)` trillion sand particles is

`Mass=1000* 6.022* 10^(11)=6.022* 10^(14)tonnes`

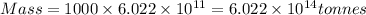
Part 2)

Since it is given that volume of 1 sand particle is
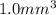`1.0mm^(3)` thus the volume of 1 mole of sand is volume of
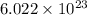`6.022* 10^(23)` sand particles

Thus volume of 1 mole is
`V=1.00* 10^(-18)km^(3)* 6.022* 10^(23)=6.022* 10^(5)km^(3)`

Now since the Area of united states is
`A=3.6* 10^(6)mile^(2)=5.8* 10^(6)km^(2)`

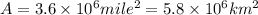
Thus the depth of the sand pile is

`Depth=(Volume)/(Area)=(6.022* 10^5)/(5.8* 10^6)=0.10387km=103.8meters`