Question

Write each equation in slope-intercept form of the equation of a line. Underline the slope and circle the y-intercept in each equation. a 3x+4y–12=0

Answer 1

`\bf 3x + 4y - 12 = 0\implies 4y-12 = -3x\implies 4y=-3x+12 \\\\\\ y = \cfrac{-3x+12}{4}\implies y = \cfrac{-3x}{4}+\cfrac{12}{4} \\\\\\ y = \stackrel{\stackrel{m}{\downarrow }}{-\cfrac{3}{4}}x\stackrel{\stackrel{b}{\downarrow }}{+3} \qquad \impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

Answer 2

The slope of the equation is:
`(-3)/(4)`

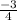
The y intercept is: 3 or (0,3)

Explanation:

Consider the provide equation of line.

`3x+4y-12=0`

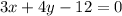
The slope intercept form is:
`y=mx+c`

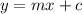
Where m is the slope and c is the y intercept.

Now convert the provided equation into slope intercept form as shown.

`4y=12-3x`

`y=(-3)/(4)x+3`

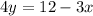
Now compare the above equation with slope intercept form.

By the comparison we can concluded that

The slope of the equation is:
`(-3)/(4)`

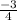
The y intercept is: 3 or (0,3)