Question

A skier starts from rest at the top of a hill. The skier coasts down the hill and up a second hill. The crest of the second hill is circular, with a radius of 36 m. Neglect friction and air resistance. What must be the height of the hill so that the skier just loses contact with the snow at the crest of the second hill?

Answer 1

18 m

Step-by-step explanation:

Minimum velocity at the top , required so that a person on a vertical circular path does not lose contact with the floor is given by

v = √gr

v = √ 9.8 x 36

= 18.78 m /s

The skier will acquire this velocity if he falls from a height H from the crest of second hill .

Loss of potential energy = gain of kinetic energy

mgH = 1/2 m v²

H =
`(v^2)/(2g)`

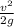
= 18.78 x 18.78 / 2 x 9.8

= 18 m .