Question

Mary's 25th birthday is today, and she hopes to retire on her 65th birthday. She has determined that she will need to have $4,000,000 in her retirement savings account in order to live comfortably. Mary currently has no retirement savings, and her investments will earn 5% annually. How much must she deposit into her account at the end of each of the next 40 years to meet her retirement savings goal?

Answer 1

Annuity will be $33112.644

Step-by-step explanation:

We have given future value ( FV ) = $4000000

Rate of interest r = 5% = 0.05

Number of periods n = 40

We know that future value is given by
`Futurte\ value(FV)=(A)/(r)[(1+r)^n-1]`

Here A is annuity

So
`4000000=(A)/(0.05)[(1+0.05)^(40)-1]`

`200000=A[(1+0.05)^(40)-1]`

`200000=A* 6.0399`

`A=$33112.644`

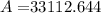
So annuity will be $33112.644