Question

A dolphin show is scheduled to start at 9:00 A.M., 9:30 A.M., and 10:00 A.M. Once the show starts, the gate will be closed. A visitor will arrive at the gate at a time uniformly distributed between 8:30 A.M. and 10:00 A.M. Determine a) The cumulative distribution function of the time (in minutes) between 8:30 A.M. and arrival.

Answer 1

The cumulative distribution function of the time (in minutes) between 8:30 A.M. and arrival is
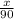`(x)/(90)` such that 0 < x < 90.

Explanation:

Consider the provided information.

A dolphin show is scheduled to start at 9:00 AM, 9:30 A.M and 10:00 A.M.

Once the show starts, the gate will be closed. The arrival time of the visitor at the gate is uniformly distributed between 8:30 A.M and 10:00 A.M.

The time in minutes is between arrival and 8:30A.M.

Uniform distribution is defined as,
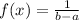`f(x) = (1)/(b-a)` where a<x<b

Here a=0 and b=90

Thus, the probability density function is:

`\left\{\begin{matrix}(1)/(90)& 0<x<90\\0& otherwise \end{matrix}\right.`

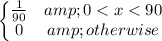
The cumulative distribution function of the time between arrival and 8.30 A.M is,

`F(X)=P(X\leq x)`

`\int\limits^x_0 {f(u)} \, du \\\int\limits^x_0 {(1)/(90)} \, du \\(1)/(90)(x-0)\\(x)/(90)`

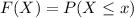
Hence, the cumulative distribution function of the time (in minutes) between 8:30 A.M. and arrival is
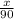`(x)/(90)` such that 0 < x < 90.