Question

The lengths of plate glass parts are measured to the nearest tenth of a millimeter. The lengths are uniformly distributed with values at every tenth of a millimeter starting at 590.2, and continuing through 590.9. Determine the mean and variance of the lengths. (a) mean (in tenths of millimeters) Round your answer to two decimal places (e.g. 98.76). (b) variance (in tenths of millimeters2) Round your answer to three decimal places (e.g. 98.765).

Answer 1

The mean of the lengths of plate glass parts is 590.55 mm or 5905.5 tenths of millimeters, and the variance is 0.04117 mm² or 4.117 tenths of millimeters².

Step-by-step explanation:

The problem involves finding the mean and variance of a uniform distribution. This distribution occurs when each value within a specific range has the same probability of occurring, as it is the case with measurements of plate glass parts rounded to the nearest tenth of a millimeter, ranging from 590.2 to 590.9.

To calculate the mean of a uniform distribution, you take the average of the maximum and minimum values. In this case:

Minimum length = 590.2 mm

Maximum length = 590.9 mm

Mean = (Minimum length + Maximum length) / 2 = (590.2 + 590.9) / 2 = 590.55 mm

The variance of a uniform distribution is given by the formula:

Variance =
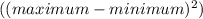`((maximum - minimum)^2)` / 12

For the plate glass lengths, this calculation is:

Variance =
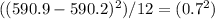`((590.9 - 590.2)^2) / 12 = (0.7^2)` / 12 = 0.04117 mm2

To express these in tenths of millimeters, we recognize that one millimeter is equivalent to ten tenths of a millimeter. So:

Mean = 590.55 mm = 5905.5 tenths of millimeters

Variance = 0.04117 mm2 = 4.117 tenths of millimeters2 (rounded to three decimal places)