Question

In a communication system the signal sent from point a to point b arrives by two paths in parallel. Over each path the signal passes through two repeaters connected in series. Each repeater in one path has a probability of failing (becoming an open circuit) of 0.002. For the other path, the probability of a repeater failing is 0.005. All repeaters fail independently of each other. Find the probability that the signal will not arrive at point b.

Answer 1

The probability is 0.00003986

Explanation:

Given an event A :

`P(A)=1-P(A^(c))`

Where
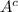`A^(c)` is the event where A does not occur

Given the following events :

Path 1 : ''The signal arrives by path 1'' where the probability of each repeater to work is 1 - 0.002 = 0.998

Path 2 : ''The signal arrives by path 2'' where the probability of each repeater to work is 1 - 0.005 = 0.995

Given two events A and B :

P(A∪B) = P(A) + P(B) - P(A∩B)

And If A and B are independent events ⇒P(A∩B) = P(A).P(B)

P(Path 1) is the probability of both repeaters from path 1 working

`P(Path 1)=0.998^(2)`

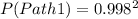
P(Path 2) is the probability of both repeaters from path 2 working

`P(Path 2) =0.995^(2)`

P(Path 1 ∩ Path 2) = P(Path 1).P(Path 2) because all repeaters fail independently

P(Path 1 ∩ Path 2) =
`(0.998^(2)).(0.995^(2))`

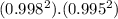
If we write the event A : ''The signal will not arrive at point b''

`P(A) =1-P(A^(c))`

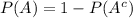
Where
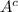`A^(c)` is the event where the signal arrives

`P(A^(c))` = P [(Path 1) ∪ (Path 2)] = P(Path 1) + P(Path 2) - P( Path 1 ∩ Path 2)

`P(A) =1-P(A^(c))\\P(A) = 1-[(0.998^(2))+(0.995^(2))-(0.998^(2))(0.995^(2))]\\P(A) = 0.00003986`