Question

An electronic product contains 53 integrated circuits. The probability that any integrated circuit is defective is 0.02, and the integrated circuits are independent. The product operates only if there are no defective integrated circuits. What is the probability that the product operates? Round your answer to four decimal places (e.g. 98.7654).

Answer 1

The probability that the product operates is 0.7807.

Step-by-step explanation:

To find the probability that the product operates, we need to find the probability that none of the integrated circuits are defective. Since each integrated circuit is independent, the probability of a circuit not being defective is 1 minus the probability of it being defective. Therefore, the probability that the product operates is the probability that all 53 integrated circuits are not defective, which is (1-0.02)^{53} = 0.7807.

Answer 2

Answer: Hello!

Here you have 53 integrated circuits, each with a probability of 0.02 of being defective.

If only one of them is defective, then the electronic product doesnt work.

Then we need the calculate the probability in wich all the 53 circuits arent defective.

the probability for each one to not be defective is 1 - 0.02 = 0.98

And if i want to see the probability for all of them to work fine, then i need to do the product of all the probabilities, this is multiply 0.98 53 times, or:

`0.98^(53) = 0.34275`

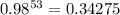
rounding to the four decimal place, we have: 0.3428

Wich is a kinda small probability for our product to work.