Question

Suppose identical tags are placed on both the left ear and the right ear of a fox. The fox is then let loose for a period of time. Consider the two events C1={left ear tag is lost} and C2={right ear tag is lost}. Let π=P(C1)=P(C2), and assume C1 and C2 are independent events. Derive an expression (involving π) for the probability that exactly one tag is lost given that at most one is lost.

Answer 1

The Probability of exactly one tag being lost, in terms of π is
`2\pi(1-\pi)-\pi^2(1-\pi)^2`

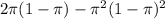
Explanation:

Using the tree diagram attached to the bottom of this answer, you can see that the probability of only one tag being lost is the union of the probability of the left tag being lost when the right one is not lost and the probability of the right tag being lost when the left one is not lost.

Probability of losing only the right tag:

`P(C2|\frac{}{C1})=P(C2)*\frac{}{P(C1)}=\pi*(1-\pi)`

Probabilty of losing only the left tag:

`P(C1|\frac{}{C2})=P(C1)*\frac{}{P(C2)}=\pi*(1-\pi)`

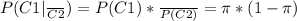
Now, to unite those two probabilities, we use basic probability properties:

`P(C2|\frac{}{C1})` ∪
`P(C1|\frac{}{C2})=P(C2|\frac{}{C1})+P(C1|\frac{}{C2})-(P(C1|\frac{}{C2})`∩
`P(C2|\frac{}{C1}))`

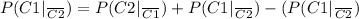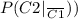
Since the events are independent:

`P(C1|\frac{}{C2})`∩
`P(C2|\frac{}{C1})=P(C1|\frac{}{C2})*P(C2|\frac{}{C1})`

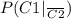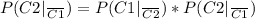
So, the union becomes:

`P(C2|\frac{}{C1})`∪
`P(C1|\frac{}{C2})=P(C1|\frac{}{C2})+P(C2|\frac{}{C1})-P(C1|\frac{}{C2})*P(C2|\frac{}{C1})`

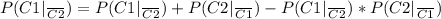
Replacing:

`=\pi(1-\pi)+\pi(1-\pi)-\pi^2(1-\pi)^2=2\pi(1-\pi)-\pi^2(1-\pi)^2`