Question

Meg's pension plan is an annuity with a guaranteed return of 7% per year (compounded quarterly). She would like to retire with a pension of $10,000 per quarter for 10 years. If she works 26 years before retiring, how much money must she and her employer deposit each quarter? HINT [See Example 5.] (Round your answer to the nearest cent.)

Answer 1

$985.92

Explanation:

In order to solve this question, we are going to use two formulas.

Present Value of an Annuity

`PV=PMT(1-(1+i)^(-n) )/(i)`

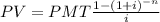
To get the value of the pension of 10,000 per quarter for 10 years. And

Sinking funds Payments Formula

`PMT=FV(i)/((1+i)^(n)-1)`

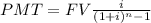
to get the Payment to be deposited each quarter during 26 years.

So for the first formula

n= number of periods = we need to know how many quarters in 10 years are. We know there are 4 quarters in a year, so 10 years multiplied by 4 is 40 quarters

n= 40

For i=interest rate= it is 7% compounded quarterly. There are 4 quarters so we divide by 4 and we get:

i=7%/4=1,75%

PMT= 10,000

`PV=10,000(1-(1+0.0175)^(-40) )/(0.0175)\\\\PV=$285,942.30`

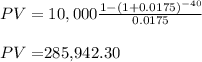
and these 285,942.30 would be our future value in the sinking fund payment formula with:

n= 26 years *(4 quarters a year)= 104 quarters

i=1.75%

FV=$285,942.30

`PMT=FV(i)/((1+i)^(n)-1)\\\\PMT=285,942.30(0.0175)/((1+0.0175)^(104)-1)\\\\PMT=985.92`

And $985.92 would have to be deposited every quarter during 26 years to get a payment of $10,000 per quarter for 10 years.