Question

A large electronic office product contains 2000 electronic components. Assume that the probability that each component operates without failure during the useful life of the product is 0.995, and assume that the components fail independently. Approximate the probability that 5 or more of the original 2000 components fail during the useful life of the product.

Answer 1

The probability is 0.971032

Explanation:

The variable that says the number of components that fail during the useful life of the product follows a binomial distribution.

The Binomial distribution apply when we have n identical and independent events with a probability p of success and a probability 1-p of not success. Then, the probability that x of the n events are success is given by:

`P(x)=(n!)/(x!(n-x)!)*p^(x)*(1-p)^(n-x)`

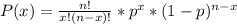
In this case, we have 2000 electronics components with a probability 0.005 of fail during the useful life of the product and a probability 0.995 that each component operates without failure during the useful life of the product. Then, the probability that x components of the 2000 fail is:

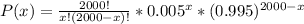`P(x)=(2000!)/(x!(2000-x)!)*0.005^(x)*(0.995)^(2000-x)` (eq. 1)

So, the probability that 5 or more of the original 2000 components fail during the useful life of the product is:

P(x ≥ 5) = P(5) + P(6) + ... + P(1999) + P(2000)

We can also calculated that as:

P(x ≥ 5) = 1 - P(x ≤ 4)

Where P(x ≤ 4) = P(0) + P(1) + P(2) + P(3) + P(4)

Then, if we calculate every probability using eq. 1, we get:

P(x ≤ 4) = 0.000044 + 0.000445 + 0.002235 + 0.007479 + 0.018765

P(x ≤ 4) = 0.028968

Finally, P(x ≥ 5) is:

P(x ≥ 5) = 1 - 0.028968

P(x ≥ 5) = 0.971032