Answer:
Option B.
Explanation:
The given inequalities are


We need to find the ordered pair which makes both inequalities true.
Check the above inequalities for each given ordered pair.
For (-3,5),
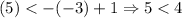 (False)
(False)
For (-2,2),
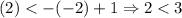 (True)
(True)
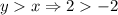 (True)
(True)
So, both inequalities are true for (-2,2). Option B is correct.
For (-1,-3),
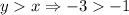 (False)
(False)
For (0,-1),
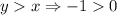 (False)
(False)
Both inequalities are not true for (-3,5), (-1,-3) and (0,-1).
Therefore, the correct option is B.