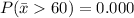Question

An airplane with room for 100 passengers has a total baggage limit of 6000 lb. Suppose that the total weight of the baggage checked by an individual passenger is a random variable x with a mean value of 49 lb and a standard deviation of 19 lb. If 100 passengers will board a flight, what is the approximate probability that the total weight of their baggage will exceed the limit? (Hint: With n = 100, the total weight exceeds the limit when the average weight x exceeds 6000/100.) (Round your answer to four decimal places.)

Answer 1

The approximate probability that the total weight of their baggage

`P (\bar x >60) = 0.000`

Explanation:

Given data;

number of passenger is 100

baggage limit = 6000 lb

standard deviation = 19 lb

mean value = 49

For 100 passengers baggage limit is 6000 lb

so, average weight for per passenger > 60

`P (\bar x >60)`

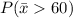
As mean value is 49, therefore
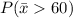`P (\bar x >60)` lie on right side center

z is given as

`z = ( \bar x \mu)/(\sigma_(\bar x))`

`z = (60 - 49)/((\sigma)/(\sqrt n))`

`z  = \frac{60 - 49}{\frac{19}{\sqrt {100}}} = 5.79`

`P(Z>5.79) = AREA to the right of 5.79`

`P (\bar x>60)  = P (Z>5.79)  = 1 -P (Z < 5.79)`

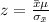
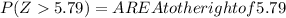
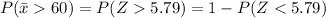
= 1 -P (Z < 5.79)

= 1 - 1.0000

= 0.000

`P (\bar x >60) = 0.000`