Question

. According to a September 2008 Harris poll, 68% of all American adults have a public library card. The percentages do differ by gender, 62% of males have library cards compared to 73% of females. (a) consider the three probabilities: P(A) = .68, P(A|B) = .62, and P(A|C) = .73. Define events A, B, C (b) Assuming that half of all Americans are males, what is the probability that an American adult is a female who owns a library card. (c) Assuming that half of all Americans are males, what is the probability that a randomly selected American adult who owns a library card is a female?

Answer 1

a) P(A) is the probability that a randomly selected American adult has a library card.

P(A/B) is the probability that a randomly selected American adult has a library card, given that he is a male.

P(A/C) is the probability that a randomly selected American adult has a library card, given that she is a female.

b) There is a 36.5% probability that an American adult is a female who owns a library card.

c) There is a 53.68% probability that a randomly selected American adult who owns a library card is a female.

Explanation:

(a) consider the three probabilities: P(A) = .68, P(A|B) = .62, and P(A|C) = .73.

P(A) is the probability that a randomly selected American adult has a library card.

P(A/B) is the probability that a randomly selected American adult has a library card, given that he is a male.

P(A/C) is the probability that a randomly selected American adult has a library card, given that she is a female.

(b) Assuming that half of all Americans are males, what is the probability that an American adult is a female who owns a library card.

There is a 50% probability that an American adult is a male and a 50% probability that an American adult is a female.

There is a 73% probability that an American adult female owns a library card.

So

`P = 0.5(0.73) = 0.365`

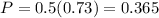
There is a 36.5% probability that an American adult is a female who owns a library card.

(c) Assuming that half of all Americans are males, what is the probability that a randomly selected American adult who owns a library card is a female?

68% of all american adults have a library card.

In b), we found that 36.5% are american female adults who own a library card.

So

`P = (0.365)/(0.68) = 0.5368`

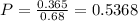
There is a 53.68% probability that a randomly selected American adult who owns a library card is a female.