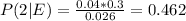Answer:
Engineer 1
Explanation:
Based on the information given:
P( 1 ) = 0.7
P( 2 ) = 0.3
P(A | B) is a conditional probability: the likelihood of event A occurring given that B is true.
P( E | 1 ) = 0.02
P( E | 2 ) = 0.04
Then P( E | 1 ) is the probability that an error occurs when engineer 1 does the work and P( E | 2 ) is the probability that an error occurs when engineer 2 does the work.
To have an idea of which engineer is more likely to do the work when an error occurs you need to calculate P( 1 | E ) and P( 2 | E ), The probability that engineer 1 does the work when an error occurs and the probability that engineer 2 does the work when an error occurs.
The Bayes's theorem states:
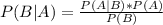
Using the notation above:
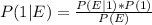
P( E ) = 0.7*0.02 + 0.3*0.04 = 0.026 /// the probability that engineer 1 does the work and an error occurs or the probability that engineer 2 does the work and an error ocurrs.
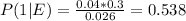
Doing the same for engineer 2: