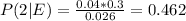Question

A construction company employs two sales engineers. Engineer 1 does the work of estimating cost for 70% of jobs bid by the company. Engineer 2 does the work for 30% of jobs bid by the company. It is known that the error rate for engineer 1 is such that 0.02 is the probability of an error when he does the work, whereas the probability of an error in the work of engineer 2 is 0.04. Suppose a bid arrives and a serious error occurs in estimating cost. Which engineer would you guess did the work? Explain and show all work.

Answer 1

Engineer 1

Explanation:

Based on the information given:

P( 1 ) = 0.7

P( 2 ) = 0.3

P(A | B) is a conditional probability: the likelihood of event A occurring given that B is true.

P( E | 1 ) = 0.02

P( E | 2 ) = 0.04

Then P( E | 1 ) is the probability that an error occurs when engineer 1 does the work and P( E | 2 ) is the probability that an error occurs when engineer 2 does the work.

To have an idea of which engineer is more likely to do the work when an error occurs you need to calculate P( 1 | E ) and P( 2 | E ), The probability that engineer 1 does the work when an error occurs and the probability that engineer 2 does the work when an error occurs.

The Bayes's theorem states:

`P( B | A ) = (P( A | B )*P( A ))/(P( B ))`

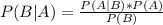
Using the notation above:

`P( 1 | E ) = (P( E | 1 )*P( 1 ))/(P( E ))`

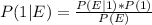
P( E ) = 0.7*0.02 + 0.3*0.04 = 0.026 /// the probability that engineer 1 does the work and an error occurs or the probability that engineer 2 does the work and an error ocurrs.

`P( 1 | E ) = (0.04*0.3)/(0.026)=0.538`

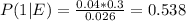
Doing the same for engineer 2:

`P( 2 | E ) = (0.04*0.3)/(0.026)=0.462`