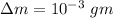Answer:
ΔP=19.76 KPa
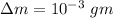
Step-by-step explanation:
Given that
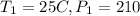
atmospheric pressure = 100 kPa.
So absolute pressure = Atmospheric pressure + gauge pressure
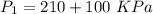 (absolute)
(absolute)
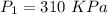 (absolute)
(absolute)
Here volume of air is constant .We know that for constant volume pressure
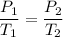
here
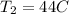
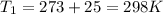
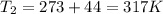
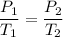
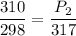
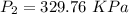 (absolute)
(absolute)
So rise in pressure
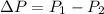
ΔP=329.76-310 KPa
ΔP=19.76 KPa
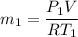
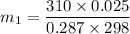
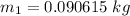
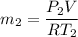
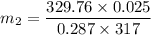
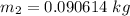
Δm=0.090615 - 0.090614 kg