Question

Write the point-slope form of the line that passes through (5,5) and is parallel to a line with a slope of 1/4 include all of your work in your final answer.

Answer 1

Answer: y - 5 = 1/4(x - 5)

Answer 2

The point-slope form of the line that passes through (5,5) and is parallel to a line with a slope of
`(1)/(4)` is x -4y +15 = 0

Solution:

The point slope form of the line that passes through the points
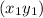`\left(x_(1) y_(1)\right)` and parallel to the line with slope “m” is given as

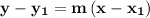`\bold{y-y_(1) = m\left(x-x_(1)\right)}` --- eqn 1

Where “m” is the slope of the line.
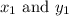`x_(1) \text { and } y_(1)` are the points that passes through the line.

From question, given that slope “m” =
`(1)/(4)`

Given that the line passes through the points (5,5).Hence we get
`x_(1)=5 ; y_(1)=5`

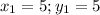
By substituting the values in eqn 1, we get the point slope form of the line which is parallel to the line having slope
`(1)/(4)` can be found out.

`y-5=(1)/(4)(x-5)`

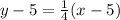
On cross multiplying we get

4y – 20 = x – 5

On rearranging, we get

x-5-4y+20 = 0

x – 4y +15 = 0

hence the point slope form the given line is x – 4y +15 = 0