Answer:
a) 17m/s; b) 21m/s; c) 23m/s; d) 29m/s; e)9m/s;
f) Line cutting at
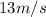 at t=0 and of slope
at t=0 and of slope
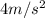
g) We also need the initial velocity.
Step-by-step explanation:
Assume a parcel of air in a straight tube moves with a constant acceleration of 4.00 m/s2 and has a velocity of 13.0 m/s at 10:05:00 a.m. on a certain date. (a) What is its velocity at 10:05:01 a.m.? (b) At 10:05:02 a.m.? (c) At 10:05:02.5 a.m.? (d) At 10:05:04 a.m.? (e) At 10:04:59 a.m.? (f) Describe the shape of a graph of velocity versus time for this parcel of air. (g) Argue for or against the statement, "Knowing the single value of an object’s constant acceleration is like knowing a whole list of values for its velocity."
We will use the equation
 , where we will start counting time from 10:05:00 a.m. This means that at that hour t=0s and our t will be the difference with that hour, and since
, where we will start counting time from 10:05:00 a.m. This means that at that hour t=0s and our t will be the difference with that hour, and since
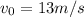 and
and
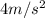 we obtain
we obtain
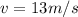 at t=0s, as expected. For each of the other parts we will have:
at t=0s, as expected. For each of the other parts we will have:
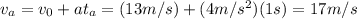

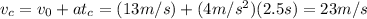

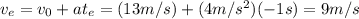
The graph of velocity versus time is a straight line cutting at
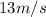 at t=0 and of slope
at t=0 and of slope
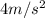 , and it's not enough to know the single value of an object’s constant acceleration to know a whole list of values for its velocity, we also need the initial velocity.
, and it's not enough to know the single value of an object’s constant acceleration to know a whole list of values for its velocity, we also need the initial velocity.