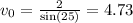Question

A golfer hits his ball with speed v o at an angle 6 above the horizontal ground. Assuming that the angle 0 is fixed and that air resistance can be neglected, what is the minimum speed v o (min) for which the ball will clear a wall of height h, a distanced away? Your solution should get into trouble if the angle 0 is such that tan 0 < h 1 d. Explain. What is v o (min) if 6 = 25°, d = 50 m, and h = 2 m?

Answer 1

The equation for the maximun height is given by the parametric equation of parabola

`h=(v_(0)^2\sin^2(\theta))/(2g)`

Explanation:

We have that

`h=v_(0)t_(h)\sin(\theta)-(1)/(2)gt{h}^2`

with

`t_(h)=(v_(0)\sin(\theta))/(g)`

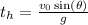
getting the general equation

`h=(v_(0)^2\sin^2(\theta))/(2g)`

For sure if the tangent of theta is less than h/d the ball doesn´t pass through the wall, this because we have the following trigonometric relation

`\tan(\theta)=(h)/(d)`

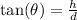
so if the tangent of theta is less than that fraction the ball won´t clear the wall.

Finally for those data we have:}

`v_(0)=(2)/(\sin(25))=4.73`