Answer:
50.2 m/s
Step-by-step explanation:
First of all, we need to find the time it takes for the ball to reach the ground.
The vertical position of the ball at time t is given by
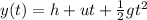
where
h = 120 m is the initial height
u = 0 is the initial vertical velocity
g = -9.8 m/s^2 is the acceleration of gravity
The ball reaches the ground when y = 0. Substituting into the equation and solving for t, we find the time of light:
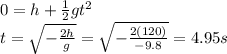
The vertical component of the velocity of the ball changes following the equation
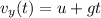
Substituting t = 4.95 s, we find the final vertical velocity of the ball just before reaching the ground:
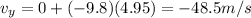
where the negative sign means the direction is downward.
We also can find the horizontal component of the velocity: since we know the horizontal distance travelled is d = 64 m,
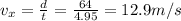
And the final speed is calculated as the magnitude of the resultant of the two components of the velocity:
