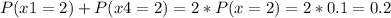Question

Answers should be exact decimals (please do not leave as fractions or unfinished calculations). A six-sided die (cube) with faces numbering 1,2,3,4,5,6 is loaded so that the probability of a six is 1/2. All the remaining numbers are equally likely.1) We roll the loaded die four times. Find the probability that... ..all the rolls are 2:none of the rolls are 2:exactly one of the rolls is a 2:at least one of the rolls is a 2:either the first roll or the last roll is a 2:

Answer 1

(a) P = 0.0001

(b) P = 0.6561

(c) P = 0.2916

(d) P = 0.3439

(e) P = 0.2

Explanation:

This is a probability problem.

The dice is rolled 4 times (n=4) and we calculate the probability of different outcomes.

The probability of a 6 in a roll is 0.5.

The probability of a 1, 2, 3, 4 or 5 in a roll is 0.5/5=0.1.

a) Outcome: all the rolls are 2.

The probability of having a 2 in a roll is 0.1, so we can calculate the probability of having a 2 in four consecutive rolls as

`P(x1=2;x2=2;x3=2;x4=2)=P(x=2)^4=0.1^4=0.0001`

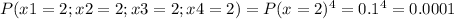
b) Outcome: none of the rolls is a 2.

The probability of having any other number but 2 in 4 rolls is:

`P(x1\\eq2;x2\\eq2;x3\\eq2;x4\\eq2)=P(x\\eq2)^4=(1-0.1)^4=0.6561`

c) Outcome: exactly one roll is a 2

This is the sum of the probability of having a 2 in the first, second, third or fouth roll, and others numbers in the rest of the rolls. These 4 combinations have the same probability, so we will multiply it by 4.

`P(exactly \,one\,2)=4*P(x1=2;x2\\eq2;x3\\eq2;x4\\eq2)\\\\P(exactly \,one\,2)=4*0.1*0.9*0.9*0.9=0.2916`

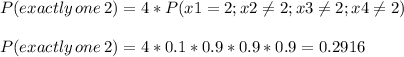
d) Outcome: at least one of the rolls is a 2

In this case, is the probability of having at least one 2, is the sum of the probability of getting a 2 in the first roll, the probability of getting a 2 in the second roll, the probability of getting a 2 in the third roll and the probability of getting a 2 in the four roll:

`P(x1=2)+P(x2=2)+P(x3=2)+P(x4=2)=0.1+0.9*0.1+0.9*0.9*0.1+0.9*0.9*0.9*0.1\\\\P(x1=2)+P(x2=2)+P(x3=2)+P(x4=2)=0.1+0.09+0.081+0.0729\\\\P(x1=2)+P(x2=2)+P(x3=2)+P(x4=2)=0.3439`

e) Outcome: either the first roll or the last roll is a 2

The probability of getting a 2 in the first roll is equal to having it in a fourth roll, and its the probability of getting a 2 in a roll (multiplied by 2, beacuse there can be either in the first or in the last roll).

`P(x1=2)+P(x4=2)=2*P(x=2)=2*0.1=0.2`