Question

Car insurance companies want to keep track of the average cost per claim. The current data in use for Auto Insurance R Us is an average of $2,200 for each claim with a standard deviation of $500. With this average, the company can stay competitive with rates but not lose money. However, the statistician for the company believes that the cost of the average claim has increased. He pulled 40 recent claims and found the average to be $2,350. Which most restrictive level of significance would suggest that the company should raise rates?

a. 1%
b. 25%
c. 5%
d. 10%

Answer 1

Answer: C. 5%

Step-by-step explanation: e22

Answer 2

5%

Explanation:

This is a significance test for a mean.

The 2 hypothesis here will be:

`H_(0): \mu = 2,200 \\H_(a): \mu > 2,200`

To determine the z-score of the error in the means you have to use this formula:

`z= (x-\mu)/((\sigma)/(√(n)) )`

`z=(2350-2200)/((500)/(√(40) ) ) =1.897`

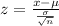
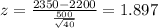
This mean that if the z score of a significance level is less than 1.897 the hypothesis that μ>2,200 is suggested.

10% -> z= 1.28

5% -> z = 1.645

1% -> z = 2.33

The most restrictive level of significance is 5%