Answer:
It would take 3225.8 hours of target detection to pay off the new controller
Step-by-step explanation:
First, to find out how many hours it would take, we calculate what is the cost per contact for both options:

Knowing the cost per contact, we calculate savings per contact when using the controller:
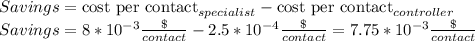
Now that we know how much the automatic controller saves, we calculate how many contacts it would take to pay it off, and then, taking into account contacts per hour, how many hours:

That means, without taking into account veteran benefits (that raise the cost of the USAF specialist), it would take around 134 days of target detection to pay off the new controller.