Answer:
Part 16) The marginal revenue is $4,000
Part 17) The marginal average cost function is (70x+41)
Explanation:
Part 16) we know that
The marginal revenue function is simply the derivative of the revenue function
we have
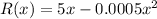
Find
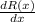
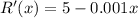
For x=1,000 units
substitute

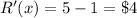
Remember that the units is in thousands of dollars
therefore
The marginal revenue is $4,000
Part 17) we know that
The marginal average cost function is simply the derivative of the average cost function
we have

Applying the distributive property
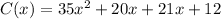
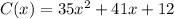
Find the derivative
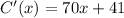
therefore
The marginal average cost function is (70x+41)