Answer:
a) 0.4567
b) 6 hours
Explanation:
We are given the following information the question:
The battery life follows a normal distribution with

Formula:
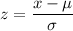
a) We have to find probability such that battery life exceeds 10 hours, that is,
P(X>10)
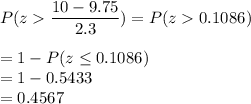
b) We have to find battery life such that
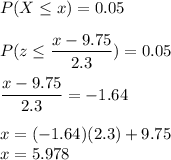
Here, we calculated the value of z from the normal distribution table.
So, after approximately 6 hours one should plan to recharge the phone.