Question

A projectile of mass M, initially at rest, is acted upon by a net force [including gravity] that increases quadratically with time as the projectile accelerates in a vertical gun barrel of length L, Fy = bt2 (1) where b is a constant. After leaving the gun barrel, the time-dependent force vanishes and the projectile rises under gravitational acceleration to a maximum height h above the end of the barrel.

Answer 1

maximum height is y = b²/18g √ (12L/b)³

Step-by-step explanation:

Let's analyze the situation first we have a projectile subjected to an acceleration depends on time, so we must use the definition of acceleration to find the speed when it is at distance L, then we will use the projectile launch equations

Acceleration dependent on t

a = dv / dt

dv = adt

∫dv =∫ (b t²) dt

v = b t³ / 3

The initial speed is zero for zero time

we use the definition of speed

v = dy / dt

dy = v dt

∫dy = ∫b t³ / 3 dt

y = b/3 t⁴ / 4

y = b/12 t⁴

we evaluate from the initial point where the height is zero for the zero time

Let's calculate the time to travel the length (y = L) of the canyon

t = (12 y / b) ¼

t = (12 L / b) ¼

Taking the time, we can calculate the projectile's output speed

v = b/3
`( (12 L / b)^(3/4)`

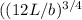
This is the speed of the body, which is the initial speed for the projectile launch movement. Let's calculate the highest point where the zero speed

Vy² = v₀² - 2 g y

0 = Vo² - 2 g y

2 g y = v₀²

y = v₀²/ 2g

y = 1/2g [b/3
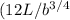`(12L / b^(3/4)`) ] 2

y = 1 / 2g [b²/9
`(12L/b)^(3/2)`]

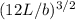y = b²/18g √ (12L/b)³