Question

A bullet is fired from a rifle that is held 3.00 m above the ground in a horizontal position. The initial speed of the bullet is 1150 m/s. There is no error in the velocity value. (a) Find the time (in s) it takes for the bullet to strike the ground. t = s (b) Find the horizontal distance (in m) traveled by the bullet. x = m (c) If the error in time measurements is Δt, what will be the equation to calculate error in the horizontal distance (Δx)? (Assume x is in meters and t is in seconds. Do not enter units in your expression. Substitute numeric values; the only variable you should enter is Δt.) Δx =

Answer 1

Answer: a) 0.78 s; b) 899.83 m; c) Δx=1150*Δt

Explanation: In order to solve this problem we have to use the kinematic equations for the independent two axis (x-y). The following expressions are:

y=yo+voy-(g*t^2)/2 g is 9.8 the aceletarion of the gravity on the y axis

vfy=voy-g*t

x=xo+vox+(a*t^2)/2 a=o there is not acceleration in the x axis.

vfx=vox+a*t

voy and vox ara the initial velocities for each axis.

yo and xo are the initial positions of teh bullet.

From these equations we can obtain the time

y=0=3-(g*t^2)/2

t^2=3*2/g

t=
`√(6/g)`

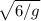
t= 0.78 s

To calculate xf= voy*t= 1150 * 0.78= 899.83 m

Finally considering with the last equation we ontain the error in Δx

in the form:

Δx=1150*Δt since is linear the dependance with time.