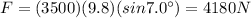Question

A 3500 kg truck is parked on a 7.0∘ slope. How big is the friction force on the truck?

Answer 1

Frictional force, f = 4180.11 N

Step-by-step explanation:

It is given that,

Mass of the truck, m = 3500 kg

It is parked on a 7 degrees slope. Let f is the frictional force acting on the truck. The force acting on it parallel to the slope is equal to the friction force required to prevent the truck from moving. It is given by :

`f=mg\ sin\theta`

`f=3500* 9.8 \ sin(7)`

f = 4180.11 N

So, the friction force on the truck is 4180.11 N. Hence, this is the required solution.

Answer 2

4180 N

Step-by-step explanation:

In order to keep the truck balanced and stationary, the force of friction on the truck must be equal to the component of the weight of the truck acting parallel to the slope.

The component of the weight of the truck acting parallel to the slope is:

`mg sin \theta`

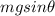
where

m = 3500 kg is the mass of the truck

g = 9.8 m/s^2 is the acceleration of gravity

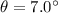`\theta=7.0^(\circ)` is the angle of the slope

Therefore, the force of friction must be equal to

`F=(3500)(9.8)(sin 7.0^(\circ))=4180 N`