Question

. A fruit company recently released a new applesauce. By the end of its first​ year, profits on this product amounted to $24,700.  The anticipated profit for the end of the fourth year is $67,900.  After the first​ year, the ratio of change in time to change in profit is constant. Let x be years and P be profit in dollars.

P(x)=
2. Find an equation of the line. Write the equation using function notation.
Through (6,−5)​; perpendicular to 4y=x-8
3. Find an equation of the line. Write the equation using function notation.
Through (-3,-8) ; parallel to 2x+3y=5
4. Find the equation of the line
Through (-11,-4) perpendicular to y=15

Answer 1

1) P(x) =14400x+10300 2)y=-4x+19 3)
`y=(-2x)/(3) -14` 4) x=-11

(Please check the pictures for better understanding)

Explanation:

1) Firstly, let's organize the data. Let the dependent variable x be the years, and the Range P(x) the Profit. So arranging these linear functions y=ax+b and plugging the coordinates for each point (1, 24700) and (4, 67900). Goes:

24,700=x+b

67,900=4x +b

1.1)Solving for b, this Linear System of Equation by the Addition Method goes:

`24,700=x+b*(-4)\\67,900=4x+b\\----------\\-98,800=-4x-4b\\67,900=4x+b\\ -----------\\-30900=-3b\\(3b)/(3) =(30900)/(3)\\ b=10300`

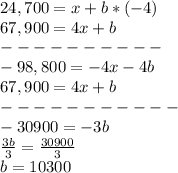
1.2) Now, let's find the slope based on those two points (1, 24700) and (4, 67900) and using the formula to find the slope:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`m=(67900-24700)/(4-1)\\ m=(43200)/(3)\\ m=14400`

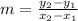
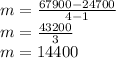
So now we can write this Linear Equation for the Profit:

P(x) =14400x+10300

2) An equation of the line perpendicular to 4y=x-8 has a slope equal to
`m_(2)`=-
`(-1)/(m_(1))` the line. In this case, an equation perpendicular to 4y=x-8 .

Rearranging the given equation of the line 4y=x-8 goes:

`y=(x)/(4) -(8)/(4) \\ y=(x)/(4)-2`

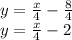
2.1) The slope of this new line is equivalent to m=-4 since -4 is opposite inverse value for the slope of its perpendicular line (1/4).

If the line passes through the point (6,-5), then this point already belongs to this line.

Then, we can write.

-5=-4(6)+b

-5=-24+b

-5+24=-24+24+b

b=19

Now we can write the function:

y=-4x+19

3) Firstly, let's rearrange the equation. Into a General Equation of the Line y=ax+b

2x+3y=5

-2x+2x+3y=5-2x

3y=5-2x

`(3y)/(3) =(5)/(3) -(2x)/(3)`

`y=(-2x)/(3)+(5)/(3)`

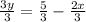
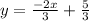
3.2) Let's find out b, the linear coefficient by plugging the coordinates of the point (-3,-8).

Also, Parallel lines have the same value for the slope such as
`m_(1)=m_(2)`

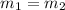
-8=-3(-2/3)+b

-8=2+b

-8-2=2-2+b

b=-10

Then the equation of this parallel line is:

`y=(-2x)/(3) -10`

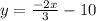
4) Now on this last question, we have to find an equation of the line through the point (-11,-4) perpendicular to another line y=15

Suppose the slope of the first line is
`m_(1)` and the value of the slope of its perpendicular is
`m_(2)=(-1)/(m_(1))`

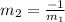
y=15 is a horizontal line with slope equals zero, we can rewrite it as y=0x+15.

Then the slope is zero for horizontal lines.

A perpendicular line to a horizontal line is a vertical one.

In addition to this, a vertical line passes through only one point in the x-axis. Then, there is no horizontal variation. This leads the formula of a slope to an undefinition for Real Set.

`m=(y_(2)-y_(1))/(0)`

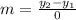
The only perpendicular line which passes through the point (-11,-4) to y=15 is the line x=-11.