Question

A batter hits a pitched ball when the center of the ball is 1.31 m above the ground.The ball leaves the bat at an angle of 45° with the ground. With that launch, the ball should have a horizontal range (returning to the launch level) of 103 m. (a) Does the ball clear a 8.55-m-high fence that is 93.0 m horizontally from the launch point? (b) At the fence, what is the distance between the fence top and the ball center?

Answer 1

Step-by-step explanation:

Given

ball is at height of 1.31 m

Horizontal Range=103 m

launch angle
`=45 ^(\circ)`

`Range=(u^2\sin 2\theta )/(g)`

`103=(u^2\sin 90)/(9.8)`

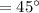
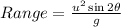
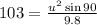
u=31.77 m/s

we know equation of trajectory of Projectile is

`y=x\tan \theta -(gx^2)/(2u^2\cos ^2 \theta )`

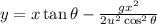
here x=93 m

`y=93* \tan 45-(9.8* 93^2)/(2* 31.77^2* \cos ^(2)45)`

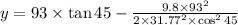
y=9.02 m

Thus at x=93 m ball is at a height of 9.02 above its initial position i.e. 10.33 m above ground

Distance between fence and height of ball=10.33-8.55=1.78 m