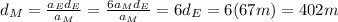Question

The acceleration due to gravity on the moon is about one-sixth its value on earth. If a baseball reaches a height of 67 m when wurth (jaw6696) – Ch 2 LT 3/4 – kreft – (61920) 2 thrown upward by someone on the earth, what height would it reach when thrown in the same way on the surface of the moon? Answer in units of m.

Answer 1

402m

Step-by-step explanation:

We can solve this easily by using the free fall formula:

`v_f^2=v_0^2+2ad`

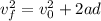
On both cases the final velocity will be 0m/s (maximum height), so we have:

`v_0^2=-2ad`

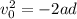
We know that the velocity the person imparts to the ball will be the same either on Earth or on the Moon, so we write for both cases:

`v_0^2=-2a_Ed_E`

`v_0^2=-2a_Md_M`

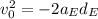
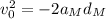
Which means

`2a_Ed_E=2a_Md_M`

So we get (taking into account that gravity on earth is 6 times gravity on the Moon):

`d_M=(a_Ed_E)/(a_M)=(6a_Md_E)/(a_M)=6d_E=6(67m)=402m`