Question

Salmon often jump waterfalls to reach their breeding grounds. Starting downstream, 2.33 m away from a waterfall 0.488 m in height, at what minimum speed must a salmon jumping at an angle of 38 ◦ leave the water to continue upstream? The acceleration due to gravity is 9.81 m/s 2

Answer 1

5.68 m/s

Step-by-step explanation:

The motion of the salmon is the same as a projectile: it is launched with an initial speed
`u` at an angle of
`\theta=38^(\circ)` above the horizontal.

The motion of the salmon consists of two indipendent motion:

- Along the horizontal direction, it is a uniform motion with constant velocity

`v_x = u cos \theta`

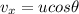
So that the distance travelled is

`d=v_x t = u cos \theta t` (1)

- Along the vertical direction, it is a uniformly accelerated motion with constant acceleration downward, so the vertical displacement is

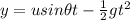`y = u sin \theta t - (1)/(2)gt^2` (2)

where g is the acceleration of gravity.

We know the following:

- The horizontal distance travelled by the salmon to reach the waterfall is

d = 2.33 m

- The vertical distance travelled is the height of the waterfall,

y = 0.488 m

From (1) we get:

`t=(d)/(u cos \theta)`

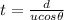
And substituting into (2), we can solve the equation to find t, the time at which the salmon reaches the waterfall:

`y = u sin \theta (d)/(u cos \theta) - (1)/(2)gt^2 = d tan \theta - (1)/(2)gt^2\\t = \sqrt{(2(d tan \theta - y))/(g)}=\sqrt{(2(2.33 tan 38^(\circ)-0.488))/(9.81)}=0.521 s`

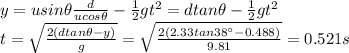
And then, we can use eq.(1) again to find the initial speed, u:

`u=(d)/(cos \theta t)=(2.33)/(cos(38^(\circ))(0.521))=5.68 m/s`